3D Spherical Analysis of BAOs¶
In this tutorial, we recover the results of [2012:Rassat] using cosmicpy.
Setting up the cosmology and the surveys¶
For this tutorial, we are going to use galaxy surveys following a Gaussian selection function of the form:
We define 2 such surveys, one shallow with \(r_0 = 100 \quad h^{-1}\) Mpc and one deep with \(r_0 = 1400 \quad h^{-1}\) Mpc:
In [1]: from cosmicpy import *
In [2]: cosmo = cosmology()
In [3]: surv_deep = survey(nzparams={'type':'gaussian', 'cosmology':cosmo, 'r0':1400}, zmax=3.0, fsky=1.0)
In [4]: surv_shallow = survey(nzparams={'type':'gaussian', 'cosmology':cosmo, 'r0':100}, zmax=0.5, fsky=1.0, chicut=0)
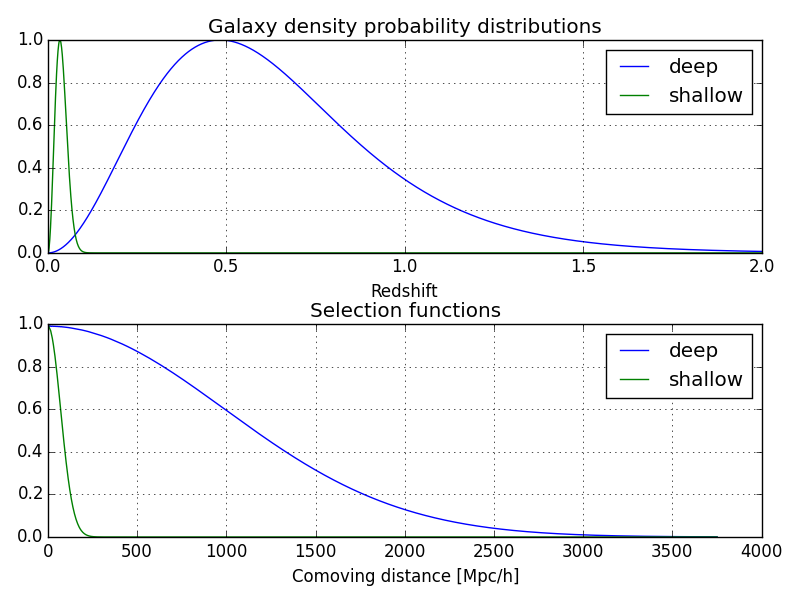
Now, we plot the selection functions along with the galaxy density probability distribution for these 2 surveys normalized by their maximum values:
# Create an array of sampling redshifts between z=0 and z=2
In [5]: z = arange(0.0001,2.0,0.001)
# Convert redshift array into comoving distance
In [6]: r = cosmo.a2chi(z2a(z))
# Compute n(z) for both survey
In [7]: pzd = surv_deep.nz(z)
In [8]: pzs = surv_shallow.nz(z)
# Compute selection function for both survey
In [9]: phid = surv_deep.phi(cosmo,r)
In [10]: phis = surv_shallow.phi(cosmo,r)
Now, let us plot the selection functions and galaxy distributions for both surveys:
In [11]: figure();
In [12]: subplot(211); xlabel('Redshift'); grid();
In [13]: plot(z,pzd/pzd.max(),label='deep');
In [14]: plot(z,pzs/pzs.max(),label='shallow');
In [15]: legend(); title('Galaxy density probability distributions');
In [16]: subplot(212); xlabel('Comoving distance [Mpc/h]'); grid();
In [17]: plot(r,phid/phid.max(),label='deep');
In [18]: plot(r,phis/phis.max(),label='shallow');
In [19]: legend(); title(r'Selection functions');
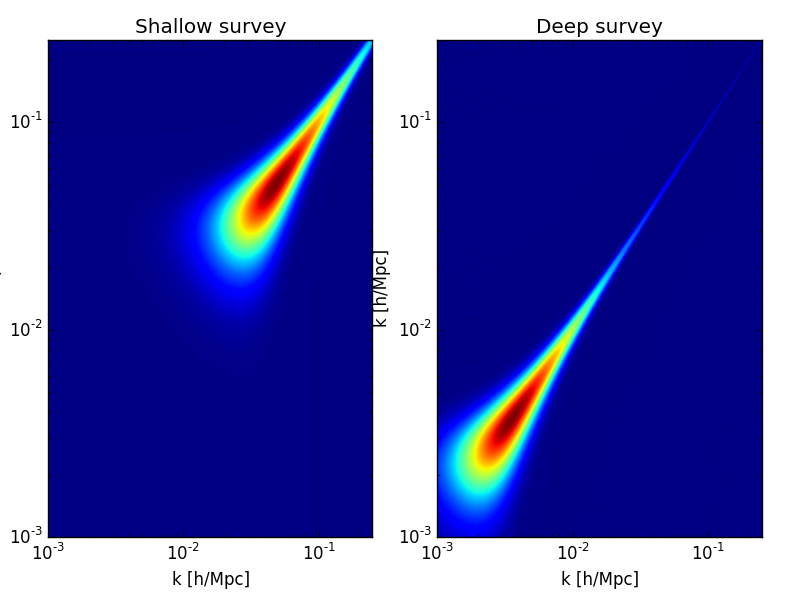
Impact of the depth of the survey on the SFB window¶
The depth of the survey directly impacts the SFB window function \(W_\ell(k, k')\) : the deeper the survey, the closer to a Dirac \(\delta(k - k')\) it becomes. We illustrate this by computing the window function for \(\ell = 3\) for the 2 surveys we consider using spectra.W() :
In [20]: k = logspace(-3,log(0.25)/log(10),512)
In [21]: sp_deep = spectra(cosmo,surv_deep)
In [22]: sp_shallow = spectra(cosmo,surv_shallow)
In [23]: subplot(121); xscale('log') ; yscale('log')
In [24]: contourf(k, k, sp_shallow.W(3, k, k), 256);
In [25]: title('Shallow survey'); xlabel('k [h/Mpc]'); ylabel('k [h/Mpc]');
In [26]: subplot(122); xscale('log') ; yscale('log')
In [27]: contourf(k, k, sp_deep.W(3, k, k), 256);
In [28]: title(r'Deep survey'); xlabel('k [h/Mpc]'); ylabel('k [h/Mpc]');
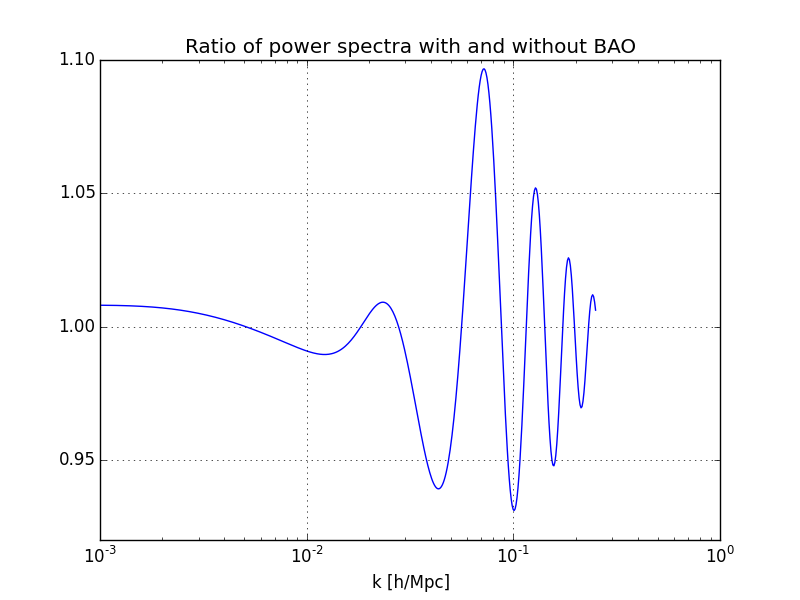
Impact of BAOs on the power spectrum¶
To emphasize the BAO features on the power spectrum, we can plot the ratio of linear power spectra today with and without BAOs. The fitting formulae used here are taken from [EisensteinHu98] . The 2 kinds of power spectra are easily computed using the cosmology.pk_lin() method:
In [29]: pk_osc = cosmo.pk_lin(k,1.0,type='eisenhu_osc')
In [30]: pk = cosmo.pk_lin(k,1.0,type='eisenhu')
In [31]: figure(); grid();
In [32]: semilogx(k,pk_osc/pk);
In [33]: xlabel('k [h/Mpc]'); title('Ratio of power spectra with and without BAO');
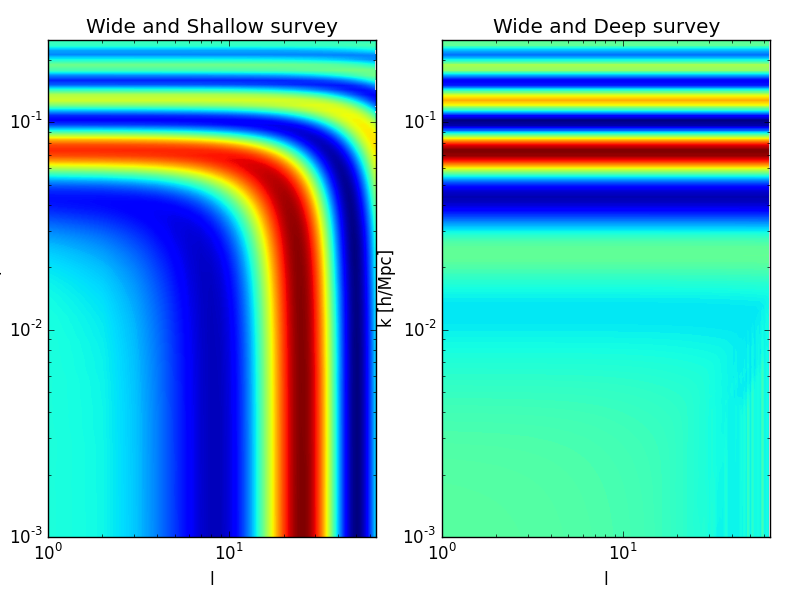
Impact of BAOs on the SFB power spectrum¶
In Spherical Fourier-Bessel space, we consider the ratio \(R_\ell^C (k)\) giben by:
where \(C_\ell^\mathrm{b}(k)\) is the diagonal SFB power spectrum including the physical effects of baryons and \(C_\ell^\mathrm{nob}(k)\) is the smooth part of the SFB power spectrum. Here we use the spectra.cl_sfb() method:
In [34]: k = logspace(-3,log(0.25)/log(10),100)
In [35]: l = arange(1,65)
In [36]: R_deep = sp_deep.cl_sfb(l,k,shotNoise=False,type='eisenhu_osc')/sp_deep.cl_sfb(l,k,shotNoise=False,type='eisenhu')
In [37]: R_shallow = sp_shallow.cl_sfb(l,k,shotNoise=False,type='eisenhu_osc')/sp_shallow.cl_sfb(l,k,shotNoise=False,type='eisenhu')
In [38]: figure(1); subplot(121); xscale('log') ; yscale('log'); xlim([1,65]);
In [39]: contourf(l,k,R_shallow.T,256);
In [40]: xlabel('l'); ylabel('k [h/Mpc]'); title(r'Wide and Shallow survey');
In [41]: subplot(122); xscale('log') ; yscale('log'); xlim([1,65]);
In [42]: contourf(l,k,R_deep.T,256);
In [43]: xlabel('l'); ylabel('k [h/Mpc]'); title(r'Wide and Deep survey');